KI-Projekt: Entwicklung einer Vorhersage der Verkaufsleistung zur optimalen Lagerhaltung für Logistik

Inhaltsverzeichnis
- Einleitung
- Datensätze
- Projektphasen
- Methoden
- Ergebnisse
Die Vorhersage (Forecast) der Verkaufsleistung ist einer der wichtigsten Anforderungen an ein Unternehmen. Um das richtige Produkt zum richtigen Zeitpunkt anbieten zu können, müssen Unternehmen die Wünsche ihrer Kunden verstehen und vorhersagen. Das Vorhersagen der Nachfrage hilft dem Lager bei der Verwaltung der Produkte. Diese Prognose spielt eine wichtige Rolle bei der Entscheidungsfindung, insbesondere in einem wettbewerbsorientierten Marktumfeld wie in der Branche Foodservices.
Unternehmen wie DHL arbeiten seit letztem Jahr bereits mit einem KI-basierten Tool zur Optimierung der Logistik von Online-Händlern. Wir von Ventzke Media haben für einen Kunden aus dem Bereich Foodservices in einer 12-monatigen Projektphase ein Machine Learning (ML) basierten Algorithmus entwickelt. In diesem Artikel möchten wir die technischen Möglichkeiten und Methoden erklären, die für die Entwicklung eines individuellen Prognose-Tools verwendet werden können.
1. Einleitung
Um eine reibungslose Produktionslinie für jedes Produkt zu gewährleisten ist es notwendig, richtige Entscheidungen zu treffen und Pläne für zukünftige Veranstaltungen zu erstellen. Die Wirksamkeit einer vom Lagerverwalter getroffenen Entscheidung hängt von der Genauigkeit der Prognose des Trends der Produkte und seiner Nachfrage auf dem gesamten Markt ab. Die Vorhersage der Nachfrage reduziert ebenfalls das mit den Geschäftsaktivitäten verbundene Risiko. Dadurch ist es leichter, effiziente Entscheidungen zu treffen. Eine gute Prognose, die den Bedarf von Produkten bestimmt, hilft außerdem bei der Kapazitätsplanung und der Verwaltung des Inventars.
Der Erfolg einer Organisation hängt von der Fähigkeit ab, zukünftige Möglichkeiten zu analysieren und die Trends zu verstehen, so dass zum richtigen Zeitpunkt geeignete Maßnahmen ergriffen werden können. Prädiktive Analysen (Verwendung historischer Daten, um zukünftige Ereignisse vorherzusagen) spielen eine wesentliche Rolle, um zukünftige Aktionen risikogerecht zu planen und zu unterstützen, sowie Chancen zu sehen und zu ergreifen. Das Ergebnis der prädiktiven Analyse wird verwendet, um Muster und Trends zu erkennen. Die Genauigkeit der Analyse hängt von der Komplexität der Daten ab. Um ein erfolgreiches Modell der Vorhersage zu haben, müssen viele Faktoren berücksichtigt werden, bevor mit der Analyse begonnen werden kann.
2. Datensätze
Um den Prozess der Effizienzverbesserung der Bestandsverwaltung zu verbessern wurde der folgende Datensatz unseres Kunden gesammelt, um eine Vorhersage zu modellieren.
Der Datensatz enthält zum Teil Details aus mehreren Regionen, die Details zum Produkt für die letzten Jahre enthalten. Das Ziel der Aufgabe besteht darin, die Verkäufe jedes Produkts im Datensatz für zukünftige Verkaufswerte zu prognostizieren.
Bereitgestellte Teiledaten für Produktdetails des Kunden
Feature Beschreibung
Teile Nr. eindeutige Identifikationsnummer des Produkts
Datum Datum des aufgezeichneten Datenpunktes
Qty Verkäufe für einen bestimmten Monat
Teiletyp Typ des Produkts
Teil desc Kurze Beschreibung des Produkts
Vorlaufzeit Latenzzeit zwischen der Einleitung und der Ausführung
3. Projektphasen
Das Projekt wurde in verschiedene Phasen unterteilt. Die Phasen sind inkrementell und Teilaufgaben können voneinander abhängig sein. Die Hauptaufgabe umfasst Unteraufgaben, deren Ausführung entscheidend ist, um einen sauberen Datensatz zu haben, mit dem man arbeiten kann. Die Datenerfassung ist eine der ersten Schritte zur Erstellung einer Prognose. Für diesen Teil wurden die Daten aus der Datenbank für den Zeitraum von 4 bis 5 Jahren entnommen. Die Daten wurden im Excel-Format in zwei getrennten Dateien zur Verfügung gestellt, die zum Sammeln der Prognosen zusammengestellt wurden.
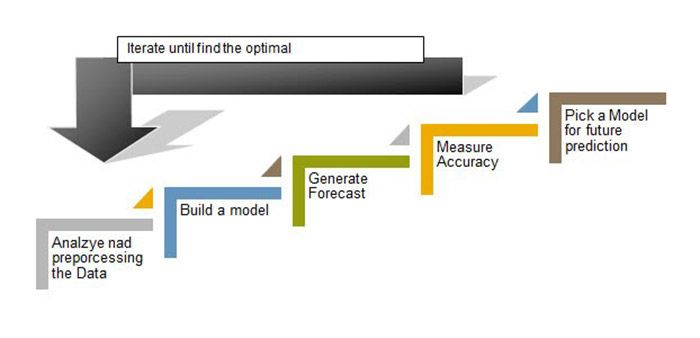
Unsere Timeline der Analyse umfasst folgende Schritte:
Analyse des gesamten zur Verfügung gestellten Teildatensätze und durchführen einiger Datenbereinigungs- und Transformationsaufgaben
Erstellen eines Basismodells aus den Merkmalen
Messen der Genauigkeit des Modells unter Verwendung der Bewertungsmatrix
Auswahl des besten Modells des Produkts für die Zukunftsprognose
A. Visualisierung
Die Datenvisualisierung spielt eine wichtige Rolle beim Verständnis des Trends und der Vorhersagen. Dies hilft zu erfahren, ob die Sequenz systematische und nicht-systematische Komponenten aufweist. Die Visualisierung der Sequenz kann auch helfen, die Komponenten der Serie zu verstehen, wie zum Beispiel die Durchschnittswerte, der Trend der steigende oder fallende Werte , die Saisonalität der sich wiederholenden Zyklen und zufällige Variationen in der Serie. Die Visualisierung hilft außerdem dabei, Ausreißer und Datenpunkte zu entfernen, sowie unvollständige, fehlerhafte oder unlogische Daten zu bereinigen.
B. Bereinigung von Daten
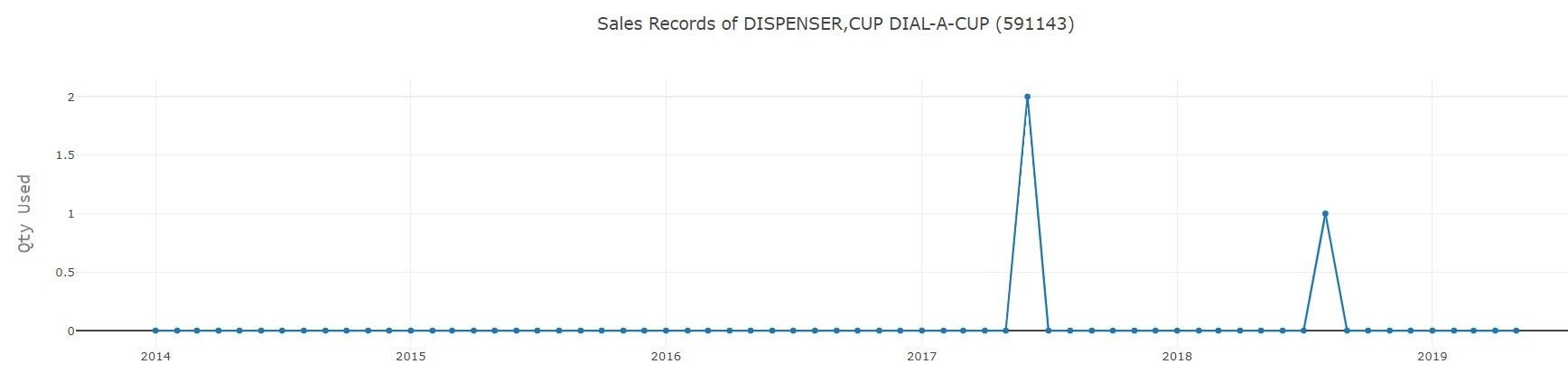
Es ist möglich, dass die gesammelten Daten den Anforderungen nicht entsprechen und einige Inkonsistenzen wie Doppelungen oder Nullwerte enthalten. Daher ist die Datenbereinigung eine wichtige Aufgabe, um die Daten konsistent zu machen. Die Datenbereinigung verbessert die Qualität der Daten und trägt somit zur Verbesserung der Ergebnisse bei. Die Daten, die in das Vorhersagemodell eingespeist werden, müssen korrekt sein und sollten das wahre Verhalten der Benutzer wiedergeben. So enthält ein Teil des Produkts Abfallwerte, die ebenfalls aus dem Datensatz entfernt werden müssen, bevor es weitergeht. Wie die Abbildung 2 veranschaulicht, enthalten viele Zeitreihen keine vollständigen Werte oder nur Werte für ein oder zwei Monate, die als Ausreißer betrachtet werden können. Dies erschwert den Prozess der Vorhersage der Werte zusätzlich, da für einen bestimmten Monat unvollständige Daten oder ein unvollständiges Produkt angefordert werden.
C. Datenreduktion
Das Grundkonzept besteht in der Reduktion der Datenmengen auf die sinnvollen Bestandteile. Die Datenreduzierung kann die Speichereffizienz erhöhen und Kosten senken. Diese Bereinigung wird bei Daten durchgeführt, die für Zeitreihenprognosen verwendet werden, so dass alle Spalten neben der verwendeten Menge und dem verwendeten Datum entfernt werden.
D. Datentransformation
Datentransformation wie Normalisierung kann die Genauigkeit und Effizienz von Lernalgorithmen verbessern, die neuronale Netze, Zeitreihenmodelle und Clustering-Klassifikatoren beinhalten. Diese Transformationen werden so eingesetzt, dass die darauf ausgeführte maschinelle Lernaufgabe genau ist und besser konvergiert, wobei auch Ausreißer ein wenig berücksichtigt werden.
1) Min-Max-Normalisierung: Führt eine lineare Transformation der ursprünglichen Datenwerte durch, wobei die Attributdaten so skaliert werden, dass sie in einen kleinen festgelegten Bereich fallen, wie z.B. [0.0 - 1.0].
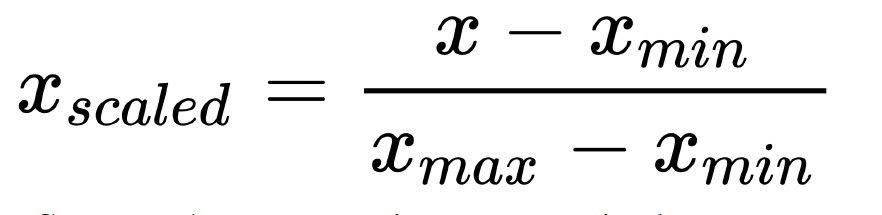
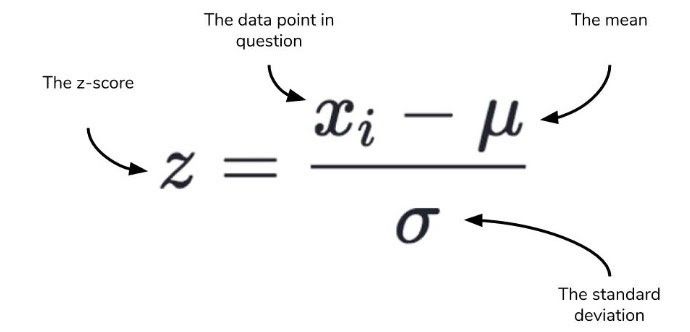
3) Python StandardScaler: Das StandardScaler ist einer der am weitesten verbreiteten Algorithmen im Python-Ökosystem. Er geht davon aus, dass Daten einer Gauß-Verteilung folgen (die Gauß-Verteilung ist dasselbe wie die Normalverteilung). Der Mittelwert und die Standardabweichung werden für das Merkmal berechnet und das Merkmal auf der Grundlage des Standard-Skalars skaliert. Die Daten werden soweit so transformiert, dass die Verteilung einen Mittelwert von 0 und eine Standardabweichung von 1 hat.
E. Basismodell
Um den Fortschritt beim Aufbau eines Machine Learning Modells zur Vorhersage der Verkaufswerte zu überprüfen, wird ein Basismodell benötigt, welches Heuristik, einfache zusammenfassende Statistiken, Zufälligkeit und maschinelles Lernen zur Erstellung von Vorhersagen für einen Datensatz verwendet. Dann wird die Vorhersage aus diesem Modell verwendet, um die Leistung des Basismodells zu messen. Im Allgemeinen besteht das Ziel hier darin, die Leistung des für die Aufgabe ausgewählten Basismodells zu übertreffen.
F. Messgenauigkeit
Die Ergebnisse der Lernalgorithmen müssen anhand von Metriken ausgewertet werden, damit sie miteinander verglichen werden können, um das beste Modell auszuwählen. Die Wahl einer passenden Metrik ist für die Aufgabe wichtig, da die gewählte Metrik bei der Klassifizierung zwar eine hohe Genauigkeit aufweisen kann, aber dennoch schlechte Ergebnisse liefert, besonders wenn man sie mit anderen Mitteln, wie dem logarithmischen Verlust oder einer anderen derartigen Metrik, vergleicht. Es gibt viele verschiedene Leistungsmaße zur Auswahl. Es kann verwirrend sein, zu wissen, welches Maß zu verwenden ist und wie die Ergebnisse zu interpretieren sind.
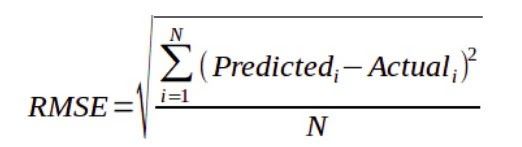
In unserem Fall konzentrieren sich Zeitreihenprognosen im Allgemeinen auf die Vorhersage realer Werte, die als Regressionsprobleme bezeichnet werden. Der mittlere absolute Fehler (MAE) und der mittlere quadratische Fehler (RMSE) sind zwei der gebräuchlichsten Metriken, die zur Messung der Genauigkeit für kontinuierliche Variablen verwendet werden. RMSE hat den Vorteil, gröbere Fehler stärker zu bestrafen, so dass sie in einigen Fällen geeigneter sein kann, z.B. wenn eine Abweichung um 10 mehr als doppelt so schlimm ist wie eine Abweichung um 5. Wenn eine Abweichung um 10 nur doppelt so schlimm ist wie eine Abweichung um 5, dann ist MAE geeigneter. Die Verwendung beider im Analysezeitraum würde also ein besseres Verständnis der dem Modell zugrunde liegenden Leistung ermöglichen, um das Modell für die Zukunftsprognose auszuwählen.
1) Mittlerer quadratischer Fehler: Er gibt die absolute Anpassung des Modells an die Daten an - Wie nahe liegen die beobachteten Datenpunkte an den vorhergesagten Werten des Modells? Residuen sind ein Maß dafür, wie weit die Regressionsgeraden von den Datenpunkten entfernt sind; der mittlere quadratische Wurzelfehler (RMSE) ist ein Maß dafür, wie diese Residuen zu verteilen sind. Er sagt also aus, wie konzentriert die Daten um die Linie der besten Anpassung herum sind. Der mittlere quadratische Fehler wird häufig in der Klimatologie, bei Vorhersagen und in der Regressionsanalyse verwendet, um experimentelle Ergebnisse zu verifizieren, so dass er auch eine gute Wahl für die Nachfrageprognose ist.
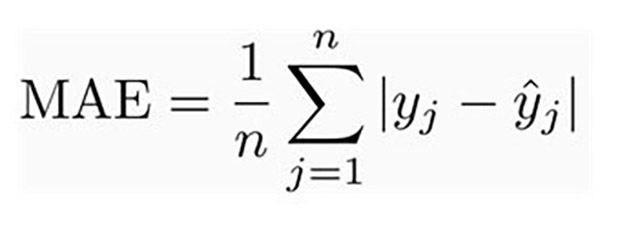
4. Methoden
Während der gesamten Projektphase wurden viele Modelle im Projekt untersucht, aber das Projekt konzentriert sich hauptsächlich auf die Durchführung umfangreicher Zeitreihenanalysen für saisonale Zersetzung, Trends, Autokorrelation usw. Die Suchspannen umfassen einfache Zeitreihenanalyse-Techniken bis hin zum Deep-Learning-Modell. In diesem Abschnitt wird auf jeden der Ansätze und seine Umsetzung eingegangen:
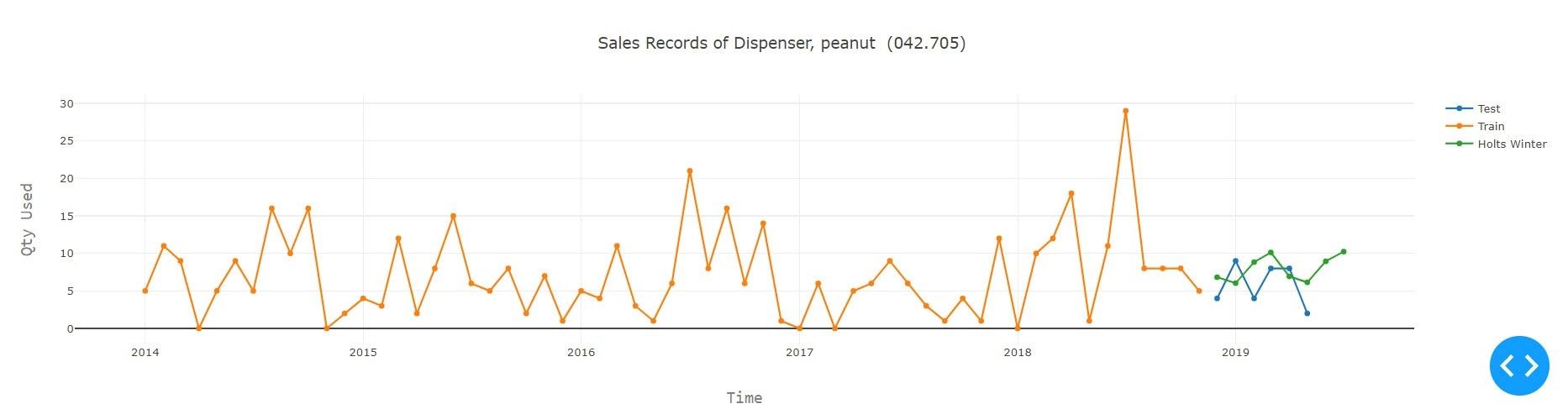
A. Holt Winters
Das Verfahren von Winters, oft auch als Holt-Winters-Verfahren bezeichnet, basiert auf dem Verfahren nach Holt und berücksichtigt zusätzlich Saisoneinflüsse. Wie das Holt-Verfahren verwendet es die exponentielle Glättung, ergänzt aber das Holt-Verfahren um die Berücksichtigung von Saisoneinflüssen.
Exponentielle Glättungsmodelle prognostizieren iterativ zukünftige Werte einer regelmäßigen Zeitreihe von Werten aus gewichteten Durchschnitten der vergangenen Werte. Bei der einfachen exponentiellen Glättung wird die nächste Stufe oder der nächste geglättete Wert aus einem gewichteten Durchschnitt des letzten tatsächlichen Wertes und des Wertes der letzten Stufe berechnet.
Saisonalität ist ein gemeinsames Merkmal von Zeitreihen. Sie kann in zwei Formen auftreten: Additiv und multiplikativ. Ein additives Modell ist ein Modell, in dem die Beiträge der Modellkomponenten summiert werden, während ein multiplikatives Modell ein Modell ist, in dem zumindest einige Komponenten multipliziert werden. Multiplikative Modelle können die Prognose für Daten verbessern, bei denen der Trend oder die Saisonalität durch das Niveau (die Größe) der Daten beeinflusst wird. Das additive Datenmodell kann die Vorhersage für Daten verbessern, bei denen der Trend oder die Saisonalität Auswirkungen einzelner Faktoren sind und diese so differenziert werden, dass sie zur Modellierung der Daten addiert werden können. Das multiplikative Modell geht davon aus, dass mit der Zunahme der Daten auch das saisonale Muster zunimmt. In diesem Modell werden die Trend- und Saisonkomponenten multipliziert und dann zur Fehlerkomponente addiert.
Um eine Auswahl zu treffen, muss tief in die Daten eingedrungen und nach einem Indikator für jedes Modell gesucht und dann entschieden werden. Wähle das multiplikatives Modell, wenn die Größenordnung des saisonalen Musters in den Daten von der Größenordnung der Daten abhängt. Wähle das additive Modell, wenn die Größenordnung des saisonalen Musters in den Daten nicht von der Größenordnung der Daten abhängt. Holt-Winters ist eine Möglichkeit, drei Aspekte der Zeitreihe zu modellieren: einen typischen Wert (Durchschnitt), eine Steigung (Trend) und ein sich zyklisch wiederholendes Muster (Saisonalität). Es gibt zwei Varianten des Modells, additiv und multiplikativ. Die additive Variation wird verwendet, wenn die saisonalen Variationen annähernd konstant sind und die multiplikative Variation wird verwendet, wenn sich die drei Aspekte proportional zum Niveau der Reihe ändern.
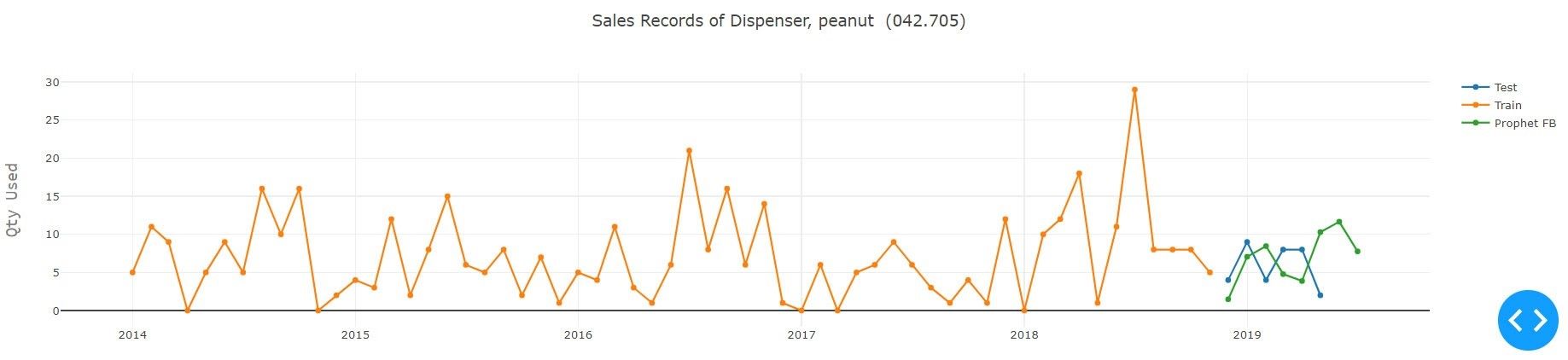
B. Vorhersage mit Facebook-Prophet
Man kann Prognosen auch mit Prophet, einem von Facebook entwickelten Tool, erstellen, um in diesem Fall die nächste N-Woche des Verkaufs vorauszusagen. Der Prophet ist eine Open-Source-Software, welche in Python und R verfügbar ist. Es basiert auf einem additiven Modell, bei dem nichtlineare Trends mit der jährlichen und wöchentlichen Saisonalität, sowie den Feiertagen übereinstimmen. Es funktioniert am besten mit den Zeitreihen, die starke saisonale Effekte und mehrere Jahreszeiten mit historischen Daten aufweisen. Prophet ist robust gegenüber fehlenden Daten und Trendverschiebungen und geht in der Regel gut mit Ausreißern um. Prophet eignet sich am besten für saisonale Datensätze, die stark mit Saisonalitäten auf menschlicher Skala verbunden sind (z.B. Modellierung für jährliche Feiertage, Neujahr) und auch unregelmäßige Intervalle in den Datensätzen berücksichtigt (verursacht durch Ereignisse wie den Super-Bowl). Diese Vorhersage mit der Prophet-Technik hat eine sehr nützliche Funktion bei der Modellierung von Feiertagen, dennoch kann die Granularität der Daten über Monate variieren, so dass die Verwendung dieser Funktion in unserem Modell nicht einfach war, da die Produkte aus verschiedenen Regionen stammen. Um genaue Daten für jedes Produkt zu erhalten, muss die Abstammungslinie jedes Produkts berücksichtigt werden.
Die Abbildung zeigt die Vorhersage mit Prophet. Die grüne Linie ist der vorausgesagte Umsatz für einen bestimmten Zeitraum, während die gelbe Linie die für das Training verwendete Sequenz und die blaue Linie die Testsequenz durch den Propheten zeigt. Wie aus der Grafik ersichtlich ist, fängt Prophet die Trends ein und die meiste Zeit erhält er die richtigen Zukunftswerte, was auch den saisonalen Trend (tägliches, wöchentliches und jährliches Muster) einfängt, dem die Daten folgen. Die verwendete Bibliotheken stammen aus numpy, pandas, fbprophet (Facebook). Durch die Verwendung von Prophet gelingt es, eine vernünftige, genaue Prognose zu erstellen.
Die Hauptkomponenten des Prophetenmodells sind Trend, Saisonalität und Feiertage. Unter Verwendung der Zeit als Regressor versucht Prophet, mehrere lineare und nichtlineare Funktionen der Zeit als Komponenten anzupassen. Die Modellierung der Saisonalität als additive Komponente basiert auf dem gleichen Ansatz wie die exponentielle Glättung.
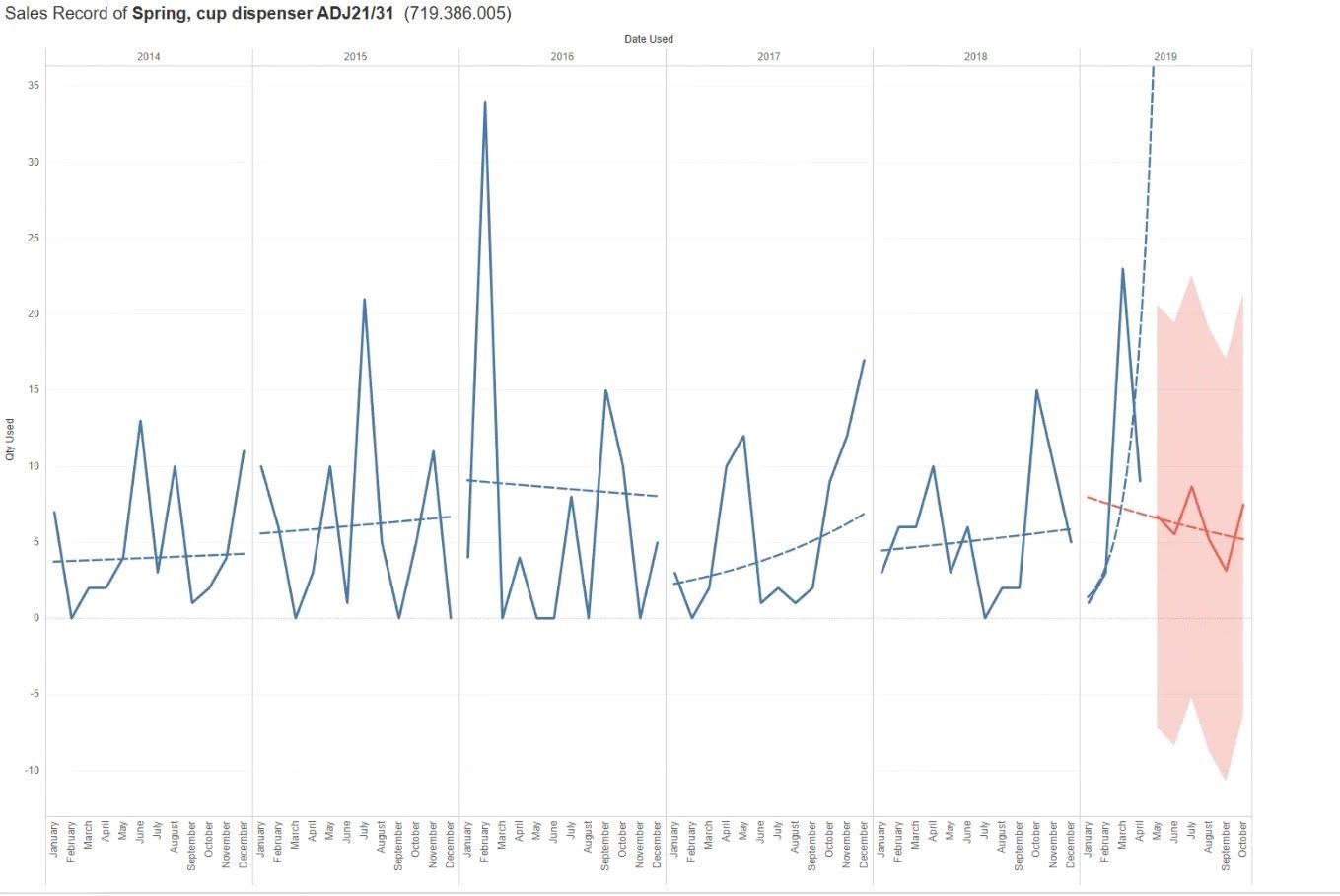
C. Vorhersagen mit Tableau
Tableau hat vor kurzem eine integrierte Vorhersage in ihrem Tool vorgestellt. Die Vorhersage mit Tableau verwendet eine Technik, die als exponentielle Glättung bekannt ist. Tableau wählt das beste Modell aus, welches sich in einem Pool von 8 Modellen befindet, wobei das beste dasjenige ist, das die qualitativ hochwertigste Vorhersage erzeugen kann.Wenn nicht genügend Daten in der Visualisierung vorhanden sind, versucht Tableau automatisch, die Prognose mit einer feineren zeitlichen Granularität zu erstellen und aggregiert die Prognose dann wieder auf die Granularität der Visualisierung.
Wenn eine Prognose mit Tableau erstellt wird, muss das Basisdatum in der Ansicht angegeben werden. Tableau verfügt über ein eingebautes Format für die Prognose, das erfüllt sein muss, damit eine gültige Prognose erstellt werden kann. Tableau-Daten unterstützen eine Reihe solcher Zeiteinheiten, einschließlich Jahr, Quartal, Monat und Tag. Die Einheit, die für den Datumswert gewählt wird, wird als Granularität des Datums bezeichnet. Die aus den Daten gewonnenen Trend- und Saisonkomponenten werden multipliziert und dann zur Fehlerkomponente addiert.
D. Autoregressiv integriert gleitender Mittelwert
Ein autoregressiver, integrierter und gleitender Mittelwert (ARIMA) ist eines der beliebtesten linearen Modelle in der Zeitreihenvorhersage. Obwohl ARIMA-Modelle insofern recht flexibel sind, als dass sie mehrere verschiedene Arten von Zeitreihen darstellen können, d.h. reine autoregressive (AR), reine gleitende Mittelwerte (MA) und kombinierte AR- und MA-Serien (ARMA), ist ihre größte Einschränkung die vorausgesetzte lineare Form des Modells. ARIMA-Modelle sind einer der am weitesten verbreiteten Ansätze zur Zeitreihenvorhersage. Sie zielen darauf ab, die Autokorrelationen in den Daten zu beschreiben.
ARIMA kann "stationär" gemacht werden, indem man sie differenziert, vielleicht in Verbindung mit nichtlinearen Transformationen wie Logging oder Deflationierung. Eine Zufallsvariable, bei der es sich um eine Zeitreihe handelt, ist stationär, wenn ihre statistischen Eigenschaften alle über die Zeit konstant sind. Eine stationäre Reihe hat keinen Trend, ihre Variationen um ihren Mittelwert herum haben eine konstante Amplitude, und sie wackelt in konsistenter Weise, d.h. ihre kurzfristigen zufälligen Zeitmuster sehen im statistischen Sinne immer gleich aus. Die letztgenannte Bedingung bedeutet, dass ihre Korrelationen mit ihren eigenen früheren Abweichungen vom Mittelwert über die Zeit konstant bleiben, oder äquivalent dazu, dass ihr Leistungsspektrum über die Zeit konstant bleibt. ARIMA(p, d, q), wobei die Parameter p, d und q nicht-negative ganze Zahlen sind, p die Ordnung des Autoregressiven Modells, d der Grad der Abweichung und q die Ordnung des Modells mit gleitendem Mittelwert ist.
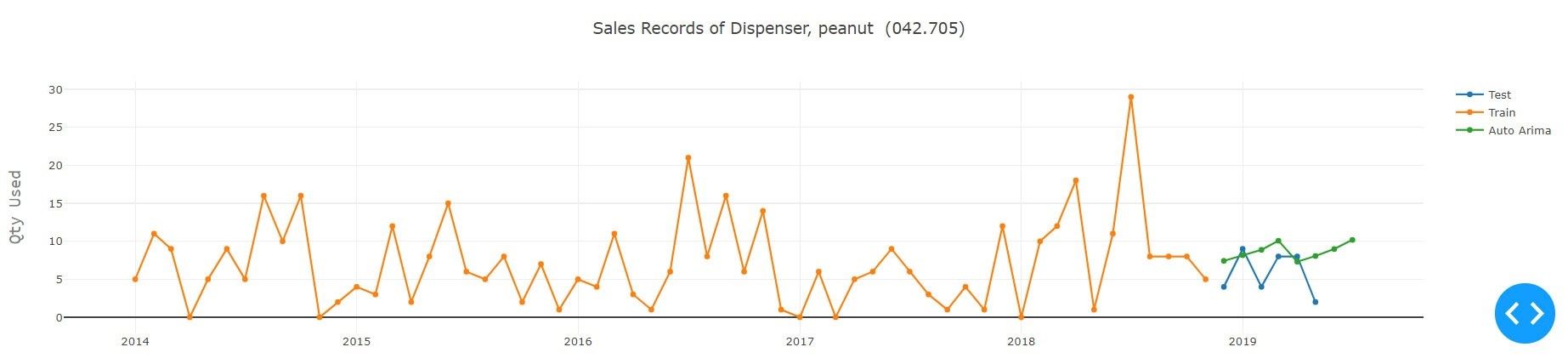
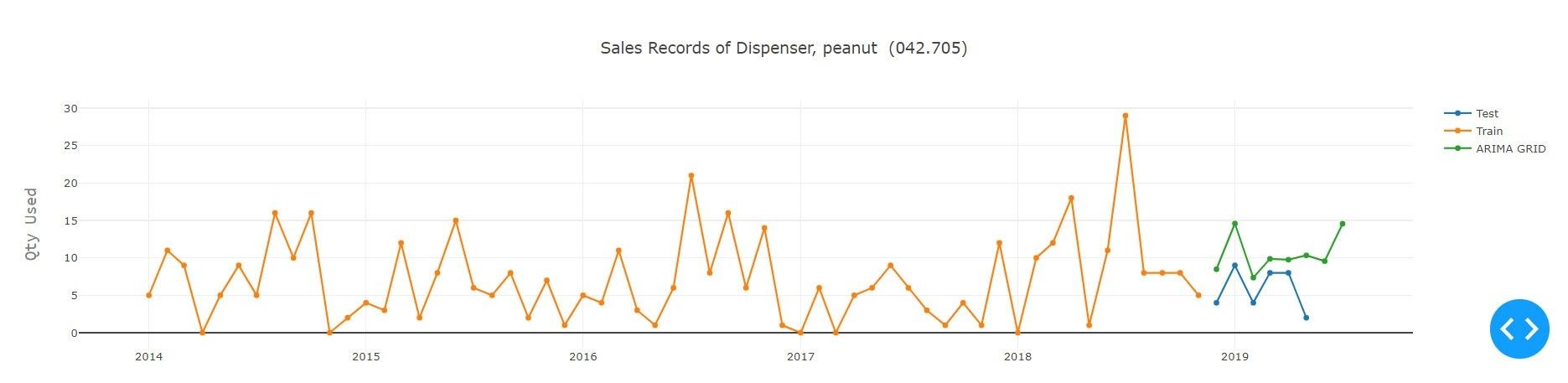
Eine andere Version des ARIMA-Modells ist SARIMA, das ebenfalls saisonale Differenzierung verwendet. Anstatt aufeinander folgende Begriffe zu subtrahieren, subtrahieren Sie den Wert von der vorherigen Saison. Das Modell wird als SARIMA (p,d,q)x(P,D,Q) dargestellt, wobei P, D und Q SAR, die Reihenfolge der Saisondifferenz bzw. SMA-Terme und 'x' die Häufigkeit der Zeitreihe entspricht. Das pmdarima-Paket bietet eine ähnliche Funktionalität. Auto-Arima verwendet einen schrittweisen Ansatz, um mehrere Kombinationen von p,d,q-Parametern zu suchen und wählt das beste Modell aus, das am wenigsten das Akaike-Informationskriterium aufweist.
AIC - Das Akaike-Informationskriterium (AIC) ist eine Schätzung der relativen Qualität von statistischen Modellen für einen gegebenen Datensatz. Somit bietet das AIC ein Mittel zur Modellauswahl. Das AIC befasst sich mit dem Kompromiss zwischen der Anpassungsgüte des Modells und der Einfachheit des Modells. Mit anderen Worten, die AIC befasst sich sowohl mit dem Risiko der Überanpassung als auch mit dem Risiko der Unteranpassung. Um den optimalen Parameter für die ARIMA-Modelle zu finden, muss aus den Daten jeder Teilsequenz ein Trainings- und Testsatz erstellen werden. Daher ist die Auswahl der letzten sechs Perioden des Datensatzes der Testsatz für unser Experiment. Dann werden die optimalen Parameter der Modelle mit Hilfe des Grid-Search-Ansatzes ausgewählt, wobei der Parameterbereich jedes einzelnen Modells definiert wird. Diese Parameter fließen in das Modell ein, in dem jedes Modell aufgebaut wird. Ausgehend von einer Sammlung von Modellen für die Daten schätzt die AIC-Modelle die Qualität jedes Modells im Verhältnis zu jedem der Anderen. Es wird das Modell mit der geringsten AIC-Punktzahl verwendet und zurückgegeben, das dann an allen Datenpunkten trainiert wird, um die zukünftigen Werte der Sequenz vorherzusagen.
E. Deeplearning
Rekurrente Netze sind künstliche neuronales Netze, die Muster in Datensequenzen erkennen sollen, wie z.B. Text, Genome, Handschrift, das gesprochene Wort oder numerische Zeitreihendaten, die von Sensoren, Aktienmärkten oder Regierungsbehörden stammen. Diese Algorithmen berücksichtigen Zeit und Sequenz, sie haben eine zeitliche Dimension.
Um rekurrente Netze zu verstehen, müssen zunächst die Grundlagen der Feedforward-Netze verstanden werden. Diese beiden Netze sind nach der Art und Weise benannt, wie sie Informationen durch eine Reihe von mathematischen Operationen kalkulieren, die an den Knoten des Netzes durchgeführt werden. Das eine Netz leitet Informationen direkt durch (wobei ein bestimmter Knoten nie zweimal berührt wird), während das andere Netz sie durch eine Schleife leitet. Letztere werden als rekurrent bezeichnet.
Im Falle von Feedforward-Netzwerken werden Input-Beispiele in das Netzwerk eingespeist und in einen Output umgewandelt werden; bei überwachtem Lernen wäre der Output ein Label, ein Name, der auf den Input angewandt wird. Das heißt, Rohdaten werden Kategorien zugeordnet und Muster erkannt, die beispielsweise signalisieren können, dass ein Bild mit "Katze" oder "Elefant" bezeichnet werden sollte. Das heißt, ein Feedforward-Netzwerk hat keine Vorstellung von zeitlicher Ordnung und die einzige Eingabe, die es berücksichtigt, ist das aktuelle Beispiel, dem es ausgesetzt ist. Feedforward-Netzwerke sind Amnesiekranke in Bezug auf ihre jüngste Vergangenheit; sie erinnern sich nostalgisch nur an die prägenden Momente des Trainings.
Rekurrente Netzwerke hingegen nehmen als Input nicht nur das aktuelle Beispiel, das sie sehen, sondern auch das, was sie vorher in der Zeit wahrgenommen haben. Hier ist ein Diagramm eines frühen, einfachen rekurrenten Netzes, das von Elman vorgeschlagen wurde, wobei die BTSXPE am unteren Rand der Zeichnung das Eingabebeispiel im aktuellen Moment und die CONTEXT UNIT, die Ausgabe des vorherigen Moments, darstellt.
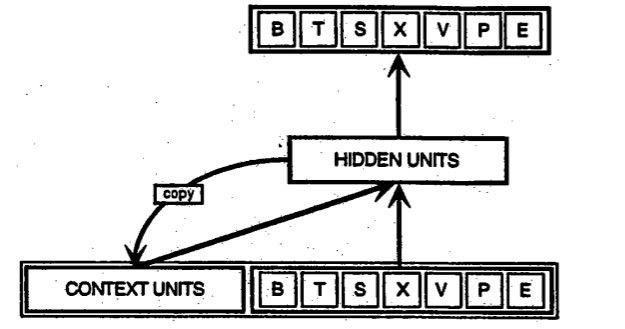
Die Entscheidung, die ein rekurrentes Netz im Zeitschritt ”t-1” getroffen hat, wirkt sich auf die Entscheidung aus, die es einen Moment später im Zeitschritt “t” treffen wird. Rekurrente Netzwerke haben also zwei Inputquellen, die Gegenwart und die jüngste Vergangenheit, die zusammen bestimmen, wie auf neue Daten reagiert wird, so wie es auch im Leben geschieht.
Rekurrente Netzwerke unterscheiden sich von Feedforward-Netzwerken durch eine Rückkopplungsschleife, die mit ihren vergangenen Entscheidungen verbunden sind und Moment für Moment ihre eigenen Ausgaben als Eingabe aufnehmen. Es wird oft gesagt, dass rekurrente Netzwerke ein Gedächtnis haben. Das Hinzufügen von Speicher zu neuronalen Netzen hat einen Zweck: Es gibt Informationen in der Sequenz selbst, welche von rekurrenten Netzen verwendet werden, um Aufgaben auszuführen, die Feedforward-Netze nicht ausführen können.
Diese sequentielle Information bleibt im verborgenen Zustand des rekurrenten Netzwerks erhalten, welches es schafft, viele Zeitschritte zu überbrücken, während es sich kaskadenartig vorwärts bewegt, um die Verarbeitung jedes neuen Beispiels zu beeinflussen. Es werden Korrelationen zwischen Ereignissen gefunden, die durch viele Momente getrennt sind. Diese werden als "langfristige Abhängigkeiten" bezeichnet, weil ein zeitlich nachgeschaltetes Ereignis von einem oder mehreren vorhergehenden Ereignissen abhängt und eine Funktion davon ist. Eine Möglichkeit, über RNNs nachzudenken, ist folgende: Sie sind eine Möglichkeit, Gewichte im Laufe der Zeit zu teilen.
Mitte der 90er Jahre wurde eine Variante des rekurrenten Netzes mit sogenannten Long Short-Term Memory Units (LSTMs) vorgeschlagen. LSTMs tragen dazu bei, Fehler zu vermeiden, welche sich über die Zeit zurückverfolgen lässt. Durch die Beibehaltung eines konstanten Fehlers wird es rekurrenten Netzen ermöglicht, über viele Zeitschritte (über 1000) hinweg weiter zu lernen, wodurch ein Kanal für die Fernverbindung von Ursachen und Wirkungen geöffnet wird.
LSTMs enthalten Informationen außerhalb des normalen Flusses des rekurrenten Netzwerks in einer Gated-Zelle. Informationen können in einer Zelle gespeichert, in sie geschrieben oder aus ihr gelesen werden, ähnlich wie Daten im Speicher eines Computers. Die Zelle trifft über Tore, die sich öffnen und schließen, Entscheidungen darüber, was gespeichert werden soll und wann Lese-, Schreib- und Löschvorgänge zugelassen werden sollen. Im Gegensatz zur digitalen Speicherung auf Computern sind diese Gatter jedoch analog, implementiert mit elementweiser Multiplikation durch Sigmoide, die alle im Bereich von 0 liegen - analog hat den Vorteil, dass es differenzierbar und daher für die Rückpropagation geeignet ist. Ein Netzwerk mit Langzeit-Kurzzeitgedächtnis (LSTM) ist eines der am häufigsten verwendeten neuronalen Netz für die Zeitreihenanalyse. Die Fähigkeit des LSTM, sich frühere Informationen zu merken, macht es ideal für die vorliegende Aufgabe.
1) Datenaufbereitung: Das Problem ist so zu formulieren, dass LSTM darauf angewendet werden kann, um eine neue Sequenz für ein zukünftiges Datum zu generieren. Das LSTM-Modell geht davon aus, dass Daten in eine Eingabe- (X) und eine Ausgabekomponente (Y) unterteilt sind. Wenn die aktuellen Daten in einem Modell nicht ausreichen, muss die Erhebung erweitert werden. Dazu müssen Eingabe- und Ausgabesequenzen der aktuellen Sequenz erstellt werden, indem der Kontext hinzugefügt wird.
Betrachtet wird die gegebene univariate Sequenz: univariate Sequenz wird in die Eingabe (X) und die Ausgabe (y) unterteilt, die in die LSTM-Zellen eingespeist werden:
X Y
10, 20, 30 40
20, 30, 40 50
Dieses Konzept kann auf die Ausgabe mehrerer Outputs wie folgt erweitert werden:
X Y
10, 20, 30 40, 50
20, 30, 40 50, 60
Dazu wird der Ausgangsvektor des Modells als Mehrschrittprognose interpretiert.
2) Modell-Ausbildung: Um die Architektur des LSTM-Modells abzuschließen, muss mit einer einfachen LSTM mit minimalen Neuronen begonnen werden. Danach geht es um den Aufbau einer komplexen LSTM-Struktur für die Zeitreihenanalyse, die die Dropout-Schicht, die L1-, L2-Regulierung, die bidirektionale LSTM, die gestapelte LSTM, die Encoder- und Decoder-LSTM-Architektur und deren hybride Kombination umfasst, um die optimale Lösung zu finden. Alle oben genannten Modelle werden in Daten eingespeist, die mit einer der oben genannten Techniken bereinigt und vorbereitet werden. Bei all den oben genannten Konfigurationen, Hyperparametern und Architekturen war es nicht trivial, das beste Modell zu wählen. Versuch und Irrtum mit all der Konfiguration, den Hyperparametern und der Implementierung verschiedener Sequenzlängen mit unterschiedlicher Architektur muss getestet werden, um zu sehen, welches Modell die anderen übertrifft. Tiefgehende Lernmodelle erfordern viel Zeit und Ressourcen, um die beste Lösung zu finden, aber am Ende erhalten Sie ein zufriedenstellendes Ergebnis, auf das Sie sich freuen können.
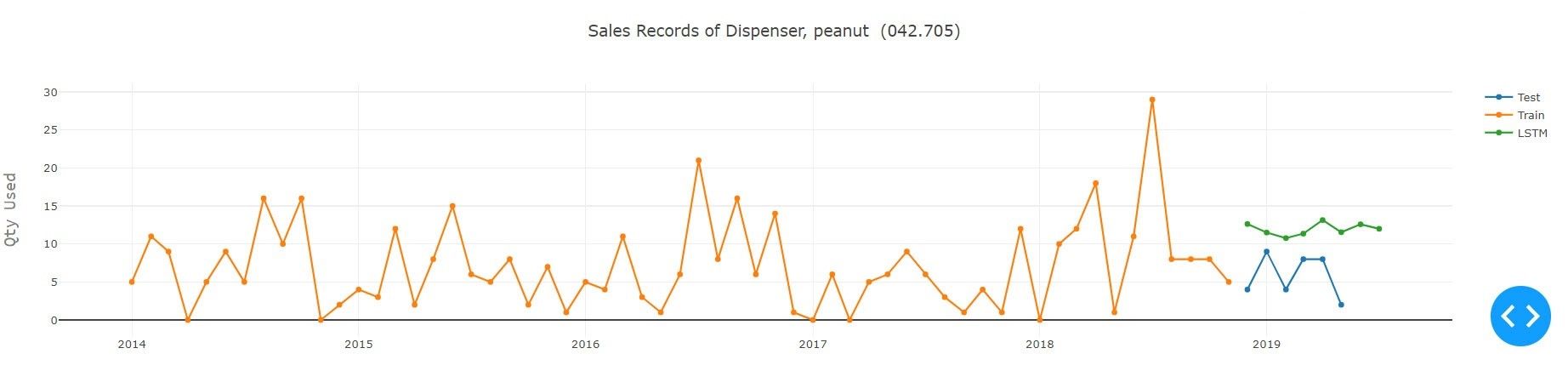
3) Einfache LSTM: Eine einfache LSTM ist ein LSTM-Modell mit einer einzelnen verborgenen Schicht von LSTM-Einheiten und einer Ausgabeschicht, die zur Erstellung einer Vorhersage verwendet wird.
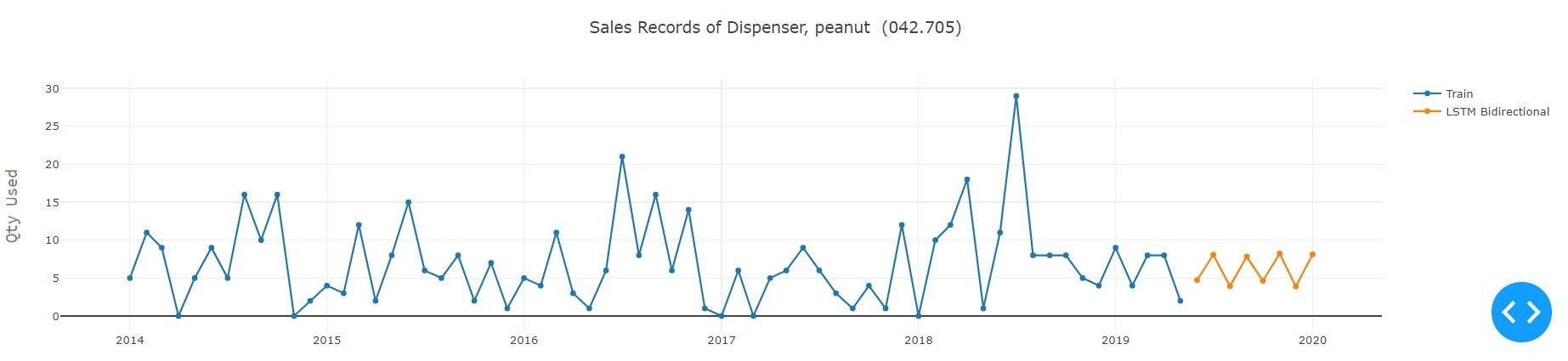
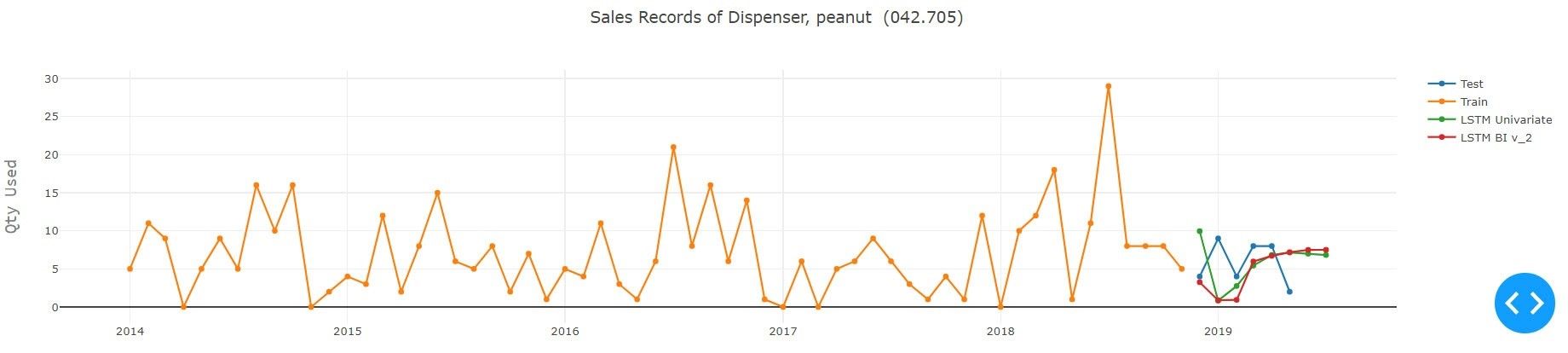
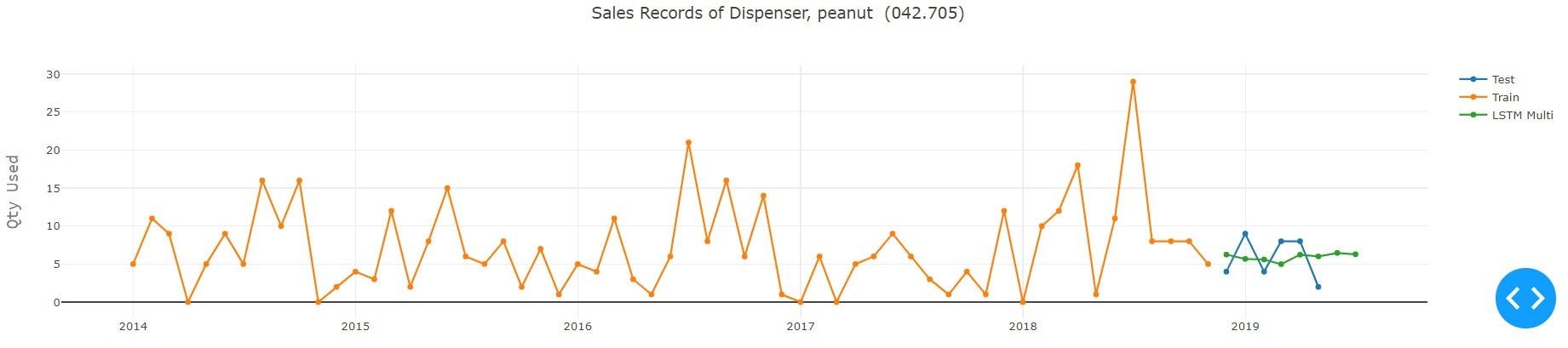
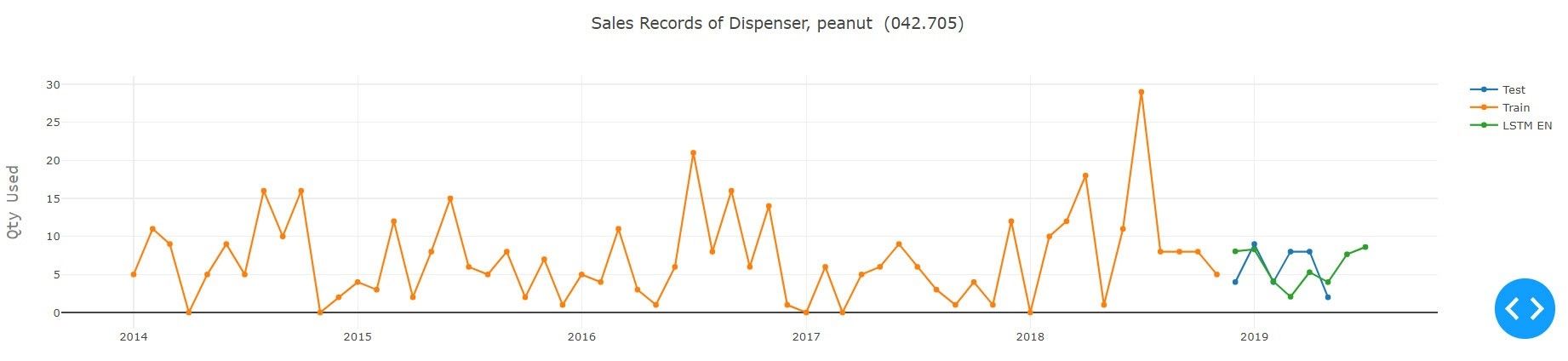
5. Ergebnisse und Schlussfolgerung
Wie aus dem obigen Experiment hervorgeht, das unter Verwendung aller verfügbaren Modelle für den gegebenen Teiletyp durchgeführt wurde, schnitt Auto ARIMA mit Grid Search und Prophet von Facebook bei der gegebenen Serie am besten ab. Im Hinblick auf das Modell für Deeplearning übertraf Encoder-Decoder LSTM alle anderen Varianten des LSTM, wobei die Erfassungsdetails der Serie recht gut waren. Dies fällt besonders auf, wenn man bedenkt, dass die LSTM-Modelle an alle Serien im Datensatz angepasst wurden, um ein sinnvolles Ergebnis zu erzielen. Die Methode des Deeplearning kann durch Versuch und Irrtum oder durch Implementierung der Optimierungstechniken, d.h. der Bayessche Optimierung, an die Sequenz angepasst werden. Die Architektur des Netzes und seine Parameter können verbessert werden.
Die Abstimmung des Modells und das Spielen mit der Anzahl der Sequenzein- und -ausgängen in der LSTM-Implementierung führt zu Verbesserungen des Modells. Nichtsdestotrotz erfüllen diese Techniken des Deeplearnings den anfänglichen Bedarf des Anwendungsfalles der Nachfrageprognose und geben somit auch einen Einblick in die Zukunft für die Vorhersage von Verkäufen aus den Teiledaten. Ein zuverlässiges und robustes Prognosemodell kann es Lagerhausmanagern ermöglichen, die Entscheidung zu treffen, ob ein Produkt für die Zukunft geeignet ist oder nicht.